
Diatomic molecules do not dissociate into fractionally charged atoms. As simple as this fact is, it is far less straightforward for electronic structure methods to adhere to this, and many approximate methods wrongly distribute charges and spins fractionally on the constituent atoms upon dissociation. Such methods break the constancy condition for fractional atomic spins, which requires systems with fractional atomic spins to have an energy equal to that of integer spin states upon dissociation. As approximate methods are unable to accurately describe the interaction between these degenerate spin-up and spin-down states, they have a massive error for fractional spin states, leading to an erroneous energetic disfavoring of atoms with integer spins. Such deficiencies in the physics of spin localization lie at the root of static correlation errors and cause many methods to not be applicable to other geometries than the equilibrium geometry. For example, most density functional theory methods dissociate a closed-shell H2 molecule into H atoms with half a spin-up and half a spin-down electron instead of normal H atoms in integer-spin states. Despite that the Schrödinger equation has been known for almost a hundred years, there is still no simple computationally efficient way of dealing with static correlation.
Correct behavior upon dissociation however can be achieved by constraining the atoms or subsystems. The framework to impose such constraints, developed by Mukherji and Karplus, relies on imposing a Lagrange multiplier on a feature operator (which can be any one-, or two-electron operator)
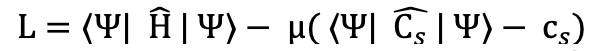
where cs is the desired value for a property C of subsystem S and Ĉs is the associated operator acting on the subsystem.
This framework can be applied to many other subsystem operators and has already culminated in many modern day applications such as, among others, constrained density functional theory, electronegativity equalization and restricted open-shell Hartree-Fock reformulated as a constrained unrestricted Hartree-Fock model.
- X De Vriendt, L Lemmens, S De Baerdemacker, P Bultinck, G Acke Quantifying Delocalization and Static Correlation Errors by Imposing (Spin)Population Redistributions through Constraints on Atomic Domains


