#include <SimpleTransformation.hpp>

Inheritance diagram for GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >:

Collaboration diagram for GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >:

Public Types
using	Scalar = _Scalar

using	DerivedTransformation = _DerivedTransformation

using	Self = SimpleTransformation< Scalar, DerivedTransformation >

using	JacobiRotationType = JacobiRotation

using	OrbitalRotationGeneratorType = typename OrbitalRotationGeneratorTraits< DerivedTransformation >::OrbitalRotationGenerators

Public Types inherited from GQCP::BasisTransformable< _DerivedTransformation >
using	Transformation = typename BasisTransformableTraits< _DerivedTransformation >::Transformation

Public Types inherited from GQCP::JacobiRotatable< _DerivedTransformation >
using	JacobiRotationType = typename JacobiRotatableTraits< _DerivedTransformation >::JacobiRotationType

Public Member Functions
	SimpleTransformation (const SquareMatrix< Scalar > &T)

	SimpleTransformation (const OrbitalRotationGeneratorType &kappa)

size_t	numberOfOrbitals () const

size_t	dimension () const

const SquareMatrix< Scalar > &	matrix () const

DerivedTransformation	adjoint () const

DerivedTransformation	inverse () const

bool	isUnitary (const double threshold=1.0e-12) const

DerivedTransformation	transformed (const DerivedTransformation &T) const override

DerivedTransformation	rotated (const JacobiRotationType &jacobi_rotation) const override

Public Member Functions inherited from GQCP::BasisTransformable< _DerivedTransformation >
virtual _DerivedTransformation	transformed (const Transformation &T) const=0

virtual void	transform (const Transformation &T)

virtual _DerivedTransformation	rotated (const Transformation &U) const

void	rotate (const Transformation &U)

Public Member Functions inherited from GQCP::JacobiRotatable< _DerivedTransformation >
virtual _DerivedTransformation	rotated (const JacobiRotationType &jacobi_rotation) const=0

void	rotate (const JacobiRotationType &jacobi_rotation)

Static Public Member Functions
static DerivedTransformation	FromJacobi (const JacobiRotation &jacobi_rotation, const size_t dim)

static DerivedTransformation	Identity (const size_t dim)

static DerivedTransformation	Random (const size_t dim)

static DerivedTransformation	RandomUnitary (const size_t dim)

static DerivedTransformation	Zero (const size_t dim)

Protected Attributes
SquareMatrix< Scalar >	T

Detailed Description

template<typename _Scalar, typename _DerivedTransformation>
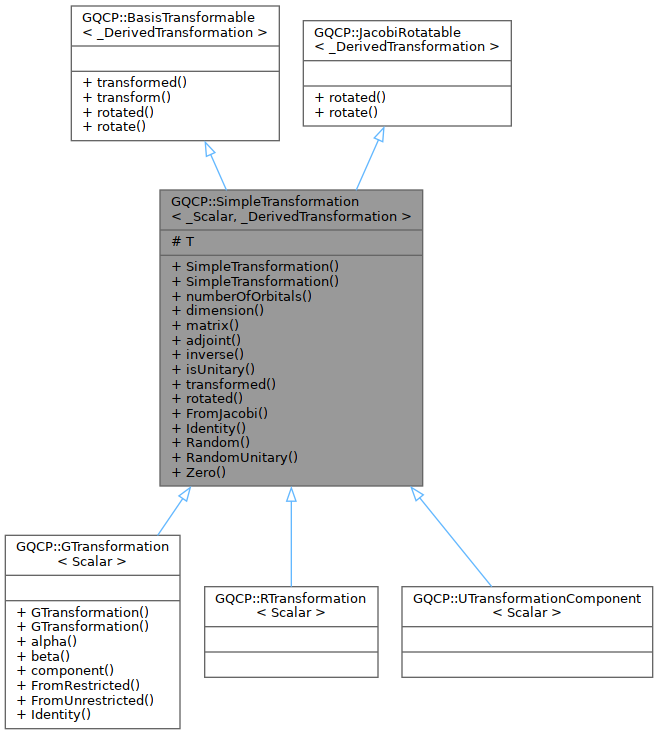
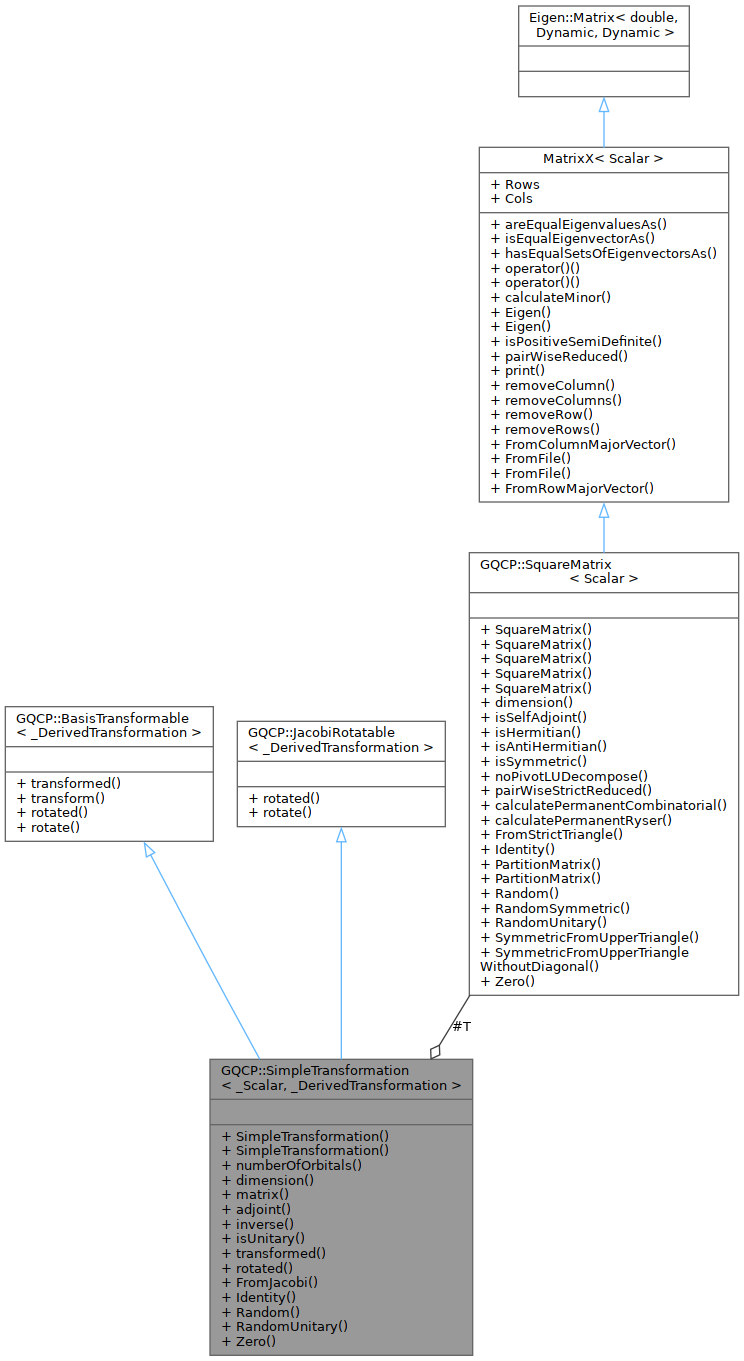
class GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >

A basis transformation that can be represented by a single transformation matrix.

In general, we adopt the convention outlined in (https://gqcg-res.github.io/knowdes/spinor-transformations.html), where the new orbitals' coefficients can be found in the respective column of the related transformation matrix.

This class is used as a base class for RTransformation and GTransformation, since they are both expressed using a single matrix, as opposed to UTransformation, which uses separate transformation coefficients for alpha- and beta- matrices. The word 'simple' is used here as an antonym for 'compound'.

Template Parameters

_Scalar	The scalar type used for a transformation coefficient: real or complex.
_DerivedTransformation	The type of the transformation matrix that derives from this class, enabling CRTP and compile-time polymorphism.

Member Typedef Documentation

◆ DerivedTransformation

template<typename _Scalar , typename _DerivedTransformation >

using GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::DerivedTransformation = _DerivedTransformation

◆ JacobiRotationType

template<typename _Scalar , typename _DerivedTransformation >

using GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::JacobiRotationType = JacobiRotation

◆ OrbitalRotationGeneratorType

template<typename _Scalar , typename _DerivedTransformation >

using GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::OrbitalRotationGeneratorType = typename OrbitalRotationGeneratorTraits<DerivedTransformation>::OrbitalRotationGenerators

◆ Scalar

template<typename _Scalar , typename _DerivedTransformation >

using GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::Scalar = _Scalar

◆ Self

template<typename _Scalar , typename _DerivedTransformation >

using GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::Self = SimpleTransformation<Scalar, DerivedTransformation>

Constructor & Destructor Documentation

◆ SimpleTransformation() [1/2]

template<typename _Scalar , typename _DerivedTransformation >

GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::SimpleTransformation ( const SquareMatrix< Scalar > & T )

inline

Construct a SimpleTransformation from the transformation matrix that it encapsulates.

Parameters

T	The transformation matrix that collects the expansion coefficients of the new basis (vectors) in the old basis as columns.

◆ SimpleTransformation() [2/2]

template<typename _Scalar , typename _DerivedTransformation >

GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::SimpleTransformation ( const OrbitalRotationGeneratorType & kappa )

inline

Construct a SimpleTransformation from a set of orbital rotation generators.

Parameters

kappa The orbital rotation generators from which a transformation so-called kappa matrix is constructed.

Member Function Documentation

◆ adjoint()

template<typename _Scalar , typename _DerivedTransformation >

DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::adjoint ( ) const

inline

Returns: The adjoint transformation of this one.

◆ dimension()

template<typename _Scalar , typename _DerivedTransformation >

size_t GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::dimension ( ) const

inline

Returns: The dimension of this basis transformation.

◆ FromJacobi()

template<typename _Scalar , typename _DerivedTransformation >

static DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::FromJacobi	(	const JacobiRotation &	jacobi_rotation,
		const size_t	dim
	)

inlinestatic

Create a general transformation from Jacobi rotation. Note that we work with the (cos, sin, -sin, cos) definition.

Parameters

jacobi_rotation	The Jacobi rotation.
dim	The dimension of the resulting matrix.

Returns: The general transformation that corresponds to the given Jacobi rotation.

◆ Identity()

template<typename _Scalar , typename _DerivedTransformation >

static DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::Identity ( const size_t dim )

inlinestatic

Create an identity transformation between two orbital bases.

Parameters

dim	The dimension of the transformation matrix.

◆ inverse()

template<typename _Scalar , typename _DerivedTransformation >

DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::inverse ( ) const

inline

Returns: The inverse transformation of this one.

◆ isUnitary()

template<typename _Scalar , typename _DerivedTransformation >

bool GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::isUnitary ( const double threshold = 1.0e-12 ) const

inline

Check if this transformation is unitary.

Parameters

threshold The threshold used to check for unitarity.

Returns: If this transformation is unitary, within the given threshold.

◆ matrix()

template<typename _Scalar , typename _DerivedTransformation >

const SquareMatrix< Scalar > & GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::matrix ( ) const

inline

Returns: The transformation matrix that collects the expansion coefficients of the new basis (vectors) in the old basis as columns.

◆ numberOfOrbitals()

template<typename _Scalar , typename _DerivedTransformation >

size_t GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::numberOfOrbitals ( ) const

inline

Returns: The number of orbitals (spinors, spin-orbitals or spatial orbitals, depending on the context/derived class) this transformation is related to.

◆ Random()

template<typename _Scalar , typename _DerivedTransformation >

static DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::Random ( const size_t dim )

inlinestatic

Create a random transformation.

Parameters

dim	The dimension of the transformation matrix.

◆ RandomUnitary()

template<typename _Scalar , typename _DerivedTransformation >

static DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::RandomUnitary ( const size_t dim )

inlinestatic

Create a random unitary transformation.

Parameters

dim	The dimension of the transformation matrix.

◆ rotated()

template<typename _Scalar , typename _DerivedTransformation >

DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::rotated ( const JacobiRotationType & jacobi_rotation ) const

inlineoverride

Apply the Jacobi rotation and return the result.

Parameters

jacobi_rotation The Jacobi rotation.

Returns: The transformation that encapsulates the sequential application of this transformation, followed by the Jacobi rotation.

◆ transformed()

template<typename _Scalar , typename _DerivedTransformation >

DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::transformed ( const DerivedTransformation & T ) const

inlineoverride

Apply the basis transformation and return the result, which corresponds to the concatenation of two basis transformations.

Parameters

T	The basis transformation.

Returns: The transformation that encapsulates the sequential application of this transformation, followed by the given transformation.

◆ Zero()

template<typename _Scalar , typename _DerivedTransformation >

static DerivedTransformation GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::Zero ( const size_t dim )

inlinestatic

Create a zero transformation.

Parameters

dim	The dimension of the transformation matrix.

Member Data Documentation

◆ T

template<typename _Scalar , typename _DerivedTransformation >

SquareMatrix<Scalar> GQCP::SimpleTransformation< _Scalar, _DerivedTransformation >::T

protected

The documentation for this class was generated from the following file:

/__w/GQCP/GQCP/gqcp/include/Basis/Transformations/SimpleTransformation.hpp

Public Types

Public Member Functions

Static Public Member Functions

Protected Attributes

Detailed Description

Member Typedef Documentation

◆ DerivedTransformation

◆ JacobiRotationType

◆ OrbitalRotationGeneratorType

◆ Scalar

◆ Self

Constructor & Destructor Documentation

◆ SimpleTransformation() [1/2]

◆ SimpleTransformation() [2/2]

Member Function Documentation

◆ adjoint()

◆ dimension()

◆ FromJacobi()

◆ Identity()

◆ inverse()

◆ isUnitary()

◆ matrix()

◆ numberOfOrbitals()

◆ Random()

◆ RandomUnitary()

◆ rotated()

◆ transformed()

◆ Zero()

Member Data Documentation

◆ T