#include <SquareMatrix.hpp>
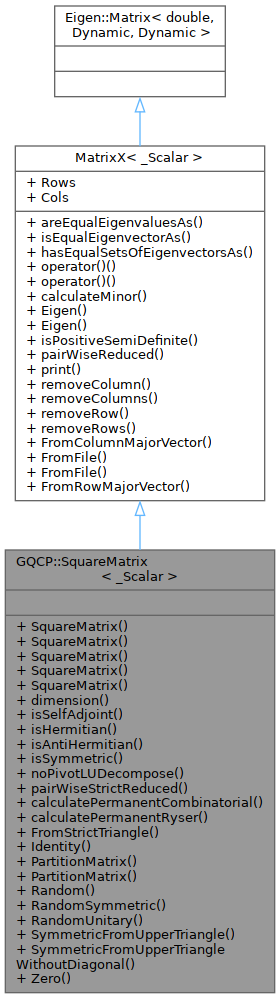
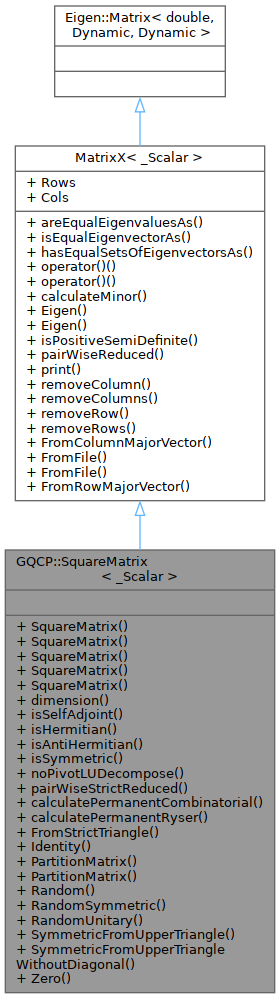
Public Types | |
| using | Scalar = _Scalar |
| using | Self = SquareMatrix< Scalar > |
 Public Types inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > Public Types inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > | |
| using | Scalar = _Scalar |
| using | Self = Matrix< Scalar, Rows, Cols > |
| using | Base = Eigen::Matrix< Scalar, Rows, Cols > |
Public Member Functions | |
| SquareMatrix () | |
| SquareMatrix (const size_t dim) | |
| SquareMatrix (const size_t rows, const size_t cols) | |
| SquareMatrix (const MatrixX< Scalar > &M) | |
| template<typename DerivedExpression > | |
| SquareMatrix (const Eigen::MatrixBase< DerivedExpression > &expression) | |
| size_t | dimension () const |
| bool | isSelfAdjoint (const double threshold=1.0e-08) const |
| bool | isHermitian (const double threshold=1.0e-08) const |
| bool | isAntiHermitian (const double threshold=1.0e-08) const |
| bool | isSymmetric (const double threshold=1.0e-08) const |
| std::array< Self, 2 > | noPivotLUDecompose () const |
| VectorX< Scalar > | pairWiseStrictReduced () const |
| double | calculatePermanentCombinatorial () const |
| double | calculatePermanentRyser () const |
 Public Member Functions inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > Public Member Functions inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > | |
| template<typename Z = bool> | |
| enable_if_t< Self::is_vector, Z > | areEqualEigenvaluesAs (const Matrix< Scalar, Dynamic, 1 > &other, double tolerance=1.0e-12) const |
| template<typename Z = bool> | |
| enable_if_t< Self::is_vector, Z > | isEqualEigenvectorAs (const Matrix< Scalar, Dynamic, 1 > &other, double tolerance=1.0e-12) const |
| template<typename Z = bool> | |
| enable_if_t< Self::is_matrix, Z > | hasEqualSetsOfEigenvectorsAs (const Matrix< Scalar, Dynamic, Dynamic > &other, double tolerance=1.0e-12) const |
| template<typename Z = Scalar> | |
| enable_if_t< Self::is_vector &&(Rows==3), Z > | operator() (const CartesianDirection direction) const |
| template<typename Z = Scalar&> | |
| enable_if_t< Self::is_vector &&(Rows==3), Z > | operator() (const CartesianDirection direction) |
| template<typename Z = Self> | |
| enable_if_t< Self::is_matrix, Z > | calculateMinor (size_t i, size_t j) const |
| const Base & | Eigen () const |
| Base & | Eigen () |
| const bool | isPositiveSemiDefinite (const double threshold=-1.0e-5) const |
| template<typename Z = Matrix<Scalar, Rows, 1>> | |
| enable_if_t< Self::is_matrix, Z > | pairWiseReduced (const size_t start_i=0, size_t start_j=0) const |
| template<typename Z = void> | |
| enable_if_t< Self::is_matrix, Z > | print (std::ostream &output_stream=std::cout) const |
| void | removeColumn (const size_t i) |
| void | removeColumns (const std::vector< size_t > &column_indices) |
| void | removeRow (const size_t i) |
| void | removeRows (const std::vector< size_t > &row_indices) |
Static Public Member Functions | |
| static Self | FromStrictTriangle (const VectorX< Scalar > &v) |
| static Self | Identity (const size_t dim) |
| static Self | PartitionMatrix (const std::vector< size_t > &indices, const size_t M) |
| static Self | PartitionMatrix (const size_t start, const size_t range, const size_t M) |
| static Self | Random (const size_t dim) |
| static Self | RandomSymmetric (const size_t dim) |
| static Self | RandomUnitary (const size_t dim) |
| static Self | SymmetricFromUpperTriangle (const VectorX< Scalar > &v) |
| static Self | SymmetricFromUpperTriangleWithoutDiagonal (const VectorX< Scalar > &v) |
| static Self | Zero (const size_t dim) |
 Static Public Member Functions inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > Static Public Member Functions inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > | |
| template<typename Z = Self> | |
| static enable_if_t<(Cols==Dynamic) &&(Rows==Dynamic), Z > | FromColumnMajorVector (const Matrix< Scalar, Dynamic, 1 > &v, const size_t rows, const size_t cols) |
| template<typename Z = Self> | |
| static enable_if_t< Self::is_vector, Z > | FromFile (const std::string &filename, size_t rows) |
| template<typename Z = Self> | |
| static enable_if_t< Self::is_matrix, Z > | FromFile (const std::string &filename, size_t rows, size_t cols) |
| template<typename Z = Self> | |
| static enable_if_t<(Cols==Dynamic) &&(Rows==Dynamic), Z > | FromRowMajorVector (const Matrix< Scalar, Dynamic, 1 > &v, const size_t rows, const size_t cols) |
Additional Inherited Members | |
 Static Public Attributes inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > Static Public Attributes inherited from GQCP::Matrix< _Scalar, _Rows, _Cols > | |
| static constexpr auto | Rows = _Rows |
| static constexpr auto | Cols = _Cols |
Detailed Description
class GQCP::SquareMatrix< _Scalar >
A square matrix. It is an extension of the Matrix class, allowing for dynamic-size square matrices.
- Template Parameters
-
_Scalar The scalar type.
Member Typedef Documentation
◆ Scalar
| using GQCP::SquareMatrix< _Scalar >::Scalar = _Scalar |
◆ Self
| using GQCP::SquareMatrix< _Scalar >::Self = SquareMatrix<Scalar> |
Constructor & Destructor Documentation
◆ SquareMatrix() [1/5]
|
inline |
The default constructor.
◆ SquareMatrix() [2/5]
|
inline |
Construct a square matrix given a dimension.
- Parameters
-
dim The dimension of the square matrix.
◆ SquareMatrix() [3/5]
|
inline |
A default constructor for Pybind11's Eigen-related casting.
- Note
- This method is only here to avoid compile-time errors with Pybind11 and should never be called directly!
◆ SquareMatrix() [4/5]
|
inline |
Construct a SquareMatrix from a GQCP::MatrixX and check the given matrix is square.
- Parameters
-
M The matrix that should be square.
◆ SquareMatrix() [5/5]
|
inline |
Construct a SquareMatrix from Eigen expressions.
- Template Parameters
-
DerivedExpression The type of the Eigen::Matrix expression, which is normally generated by the compiler.
- Parameters
-
expression The Eigen expression.
Member Function Documentation
◆ calculatePermanentCombinatorial()
|
inline |
- Returns
- the permanent using a combinatorial algorithm
◆ calculatePermanentRyser()
|
inline |
- Returns
- the permanent of the given square matrix using the Ryser algorithm
Note that this algorithm does not work for dimensions larger than 64: see https://www.codeproject.com/Articles/21282/%2FArticles%2F21282%2FCompute-Permanent-of-a-Matrix-with-Ryser-s-Algorit
◆ dimension()
|
inline |
- Returns
- the dimension of this square matrix, i.e. the number of rows or columns
◆ FromStrictTriangle()
|
inlinestatic |
- Parameters
-
a the strict (not including the diagonal) lower/upper triangle of the matrix in column major form
- Returns
- a square matrix in which the lower triangle is filled in with its given vector representation; all other elements are set to zero
◆ Identity()
|
inlinestatic |
Create an identity square matrix.
- Parameters
-
dim The dimension of the square matrix.
- Returns
- An identity square matrix.
◆ isAntiHermitian()
|
inline |
- Returns
- If this square matrix is anti-Hermitian.
◆ isHermitian()
|
inline |
- Returns
- If this square matrix is self-adjoint.
◆ isSelfAdjoint()
|
inline |
- Returns
- If this square matrix is self-adjoint.
◆ isSymmetric()
|
inline |
- Returns
- If this square matrix is symmetric.
◆ noPivotLUDecompose()
|
inline |
- Returns
- a non-pivoted LU decomposition in an array, with L at position 0 and U on position 1 of the array.
- Note
- Pivoting is required to ensure that the decomposition is stable. Eigen3 provides partial and full pivot modules, so when the pivot or permutation of a matrix is not of interest we strongly recommend using Eigen3 instead
◆ pairWiseStrictReduced()
|
inline |
- Returns
- a pair-wise strict reduced form of this square matrix. The elements of the matrix are put into the vector such that v(m) = M(i,j)
in which m is calculated from i and j in a column-major way, with the restriction that i>j
Note that this is equal to extracting to strict lower triangular matrix as a vector in column major form. Example:
5
1 5 -> (1, 2, 3)
2 3 5
◆ PartitionMatrix() [1/2]
|
inlinestatic |
- Parameters
-
start starting index of the partition range range overwhich the partition indices stretch M the dimension of the resulting matrix
- Returns
- a 'partition' matrix, which is a diagonal matrix, whose diagonal elements are either 0 or 1, as specified by the given indices
◆ PartitionMatrix() [2/2]
|
inlinestatic |
- Parameters
-
indices the indices of the diagonal which will be set to 1 M the dimension of the resulting matrix
- Returns
- a 'partition' matrix, which is a diagonal matrix, whose diagonal elements are either 0 or 1, as specified by the given indices
◆ Random()
|
inlinestatic |
Create a random square matrix.
- Parameters
-
dim The dimension of the resulting matrix.
- Returns
- A random square matrix.
◆ RandomSymmetric()
|
inlinestatic |
Create a random symmetrix matrix.
- Parameters
-
dim The dimension of the resulting matrix.
- Returns
- A random symmetric matrix.
◆ RandomUnitary()
|
inlinestatic |
Create a random unitary matrix.
- Parameters
-
dim The dimension of the resulting matrix.
- Returns
- A random unitary matrix.
◆ SymmetricFromUpperTriangle()
|
inlinestatic |
- Parameters
-
v the upper triangle (including the diagonal) of a matrix
- Returns
- the full, symmetric matrix corresponding to the given upper triangle
◆ SymmetricFromUpperTriangleWithoutDiagonal()
|
inlinestatic |
- Parameters
-
v the upper triangle (NOT including the diagonal) of a matrix
- Returns
- the full, symmetric matrix corresponding to the given upper triangle, without the diagonal.
◆ Zero()
|
inlinestatic |
Create a zero square matrix.
- Parameters
-
dim The dimension of the square matrix.
- Returns
- An zero square matrix.
The documentation for this class was generated from the following file:
- /__w/GQCP/GQCP/gqcp/include/Mathematical/Representation/SquareMatrix.hpp